
我校数理与统计学院王文涛副教授在国际学术期刊《Fuzzy Sets and Systems》上发表关于带变系数和比例时滞模糊细胞神经网络的有限时间同步的最新研究成果。
模糊细胞神经网络在心理物理学、演讲、知觉、机器人、自适应模式识别、视觉和图像处理等领域有大量应用价值,有关其稳定性、周期性和同步性有很多结果。尽管考虑到时滞对模糊细胞神经网络模型的影响,但是一般都是在常数系数以及有界时滞条件下的结果。在现实世界中,模糊细胞神经网络模型中的系数函数都不再是常数,而是变化的函数,并且时滞不是有界函数,而是无界的比例时滞。另一方面,为了控制时滞模糊细胞神经网络,有限时间同步是非常有意义的工作,因为它意味着两个或者多个系统可以在预设的有限时间内达到同步。有限时间同步的结果主要集中在常数系数和有界时滞的神经网络模型,而关于带变系数和比例时滞模糊细胞神经网络的有限时间同步还鲜有人涉及。
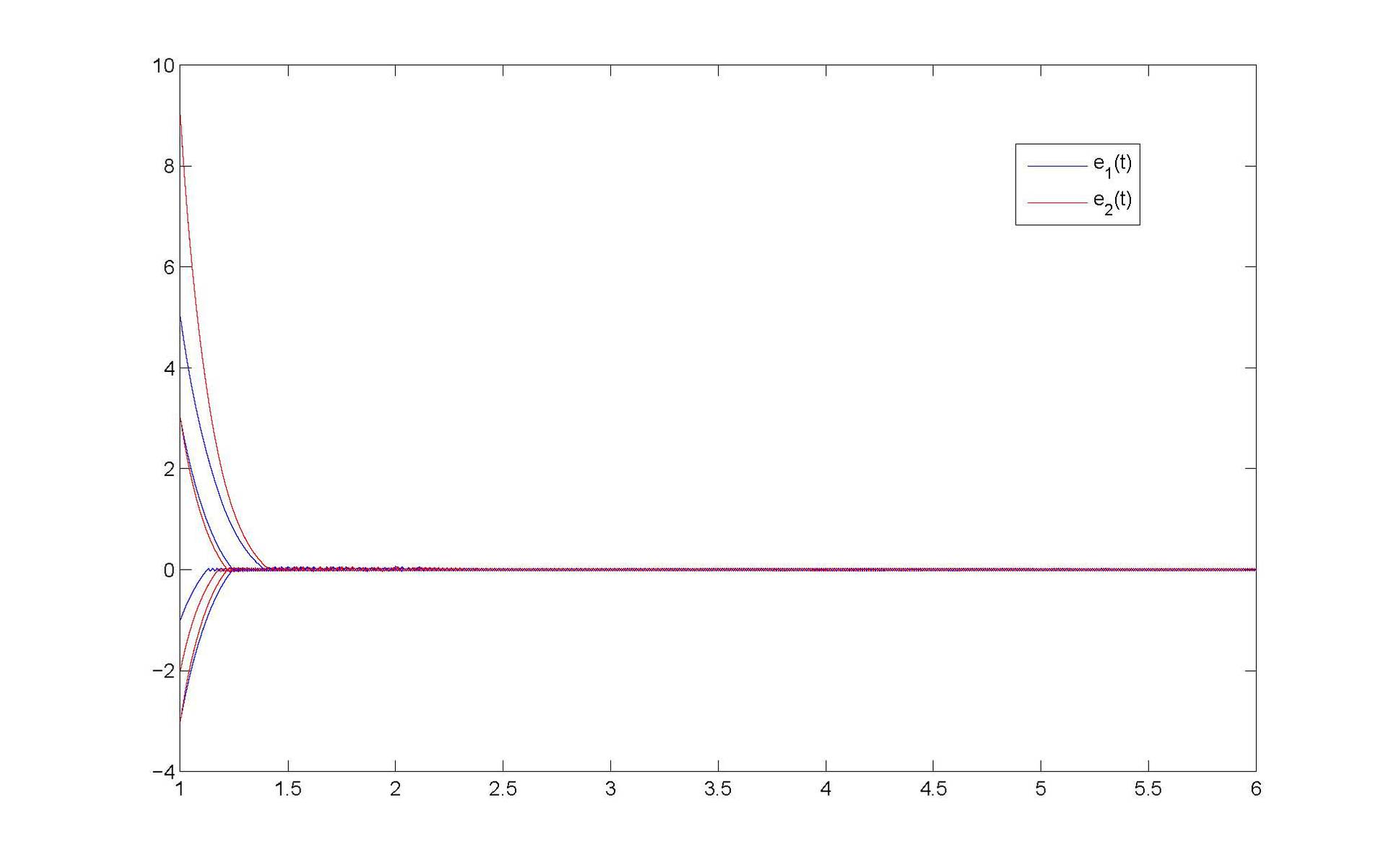
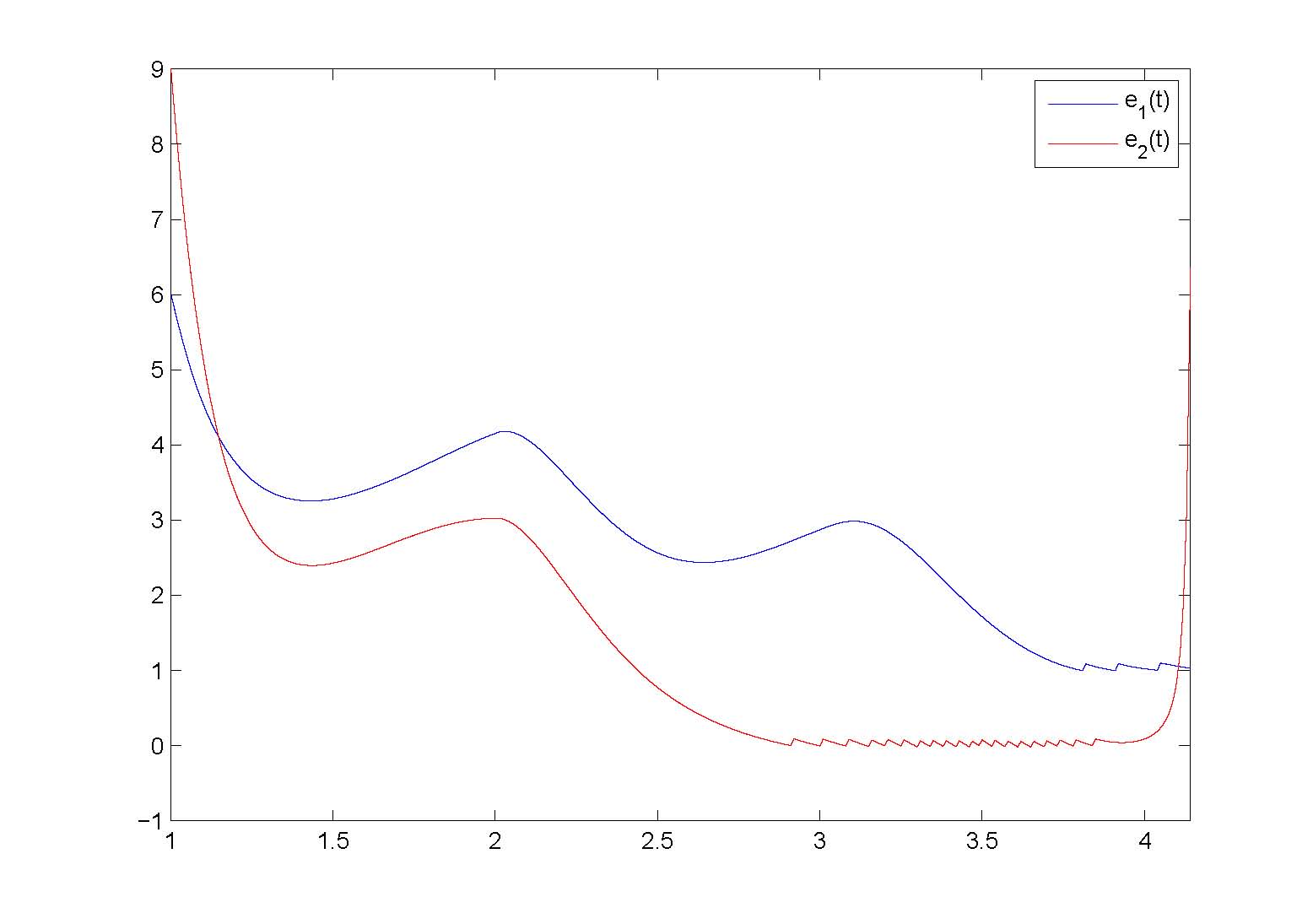
基于有限时间稳定性理论,王文涛副教授应用微分不等式和数学分析技巧,研究了一类带变系数和比例时滞模糊细胞神经网络的有限时间同步问题,获得了新的、有效的有限时间同步判断的充分性条件。最后通过一个实例和数值模拟验证了理论结果的正确性。
该研究成果以“Finite-time synchronization for a class of fuzzy cellular neural networks with time-varying coefficients and proportional delays”为题发表在《Fuzzy Sets and Systems》,主要创新点为:(1)考虑的模糊细胞神经网络模型具有变系数函数和比例时滞;(2)得到有限时间同步的显示函数表达式。《Fuzzy Sets and Systems》为ELSEVIER旗下的知名期刊,创刊于1978年,目前影响因子2.718,近5年平均影响因子2.783,是数学、应用数学和计算机领域top期刊







